In order to build a prediction model for next season I need to know how good each team was in the previous season(s). A decent and simple way to measure team quality is to use the Massey rankings, which basically just finds the points above average that each team contributes to the margin of victory of each game using Ordinary Least Squares Regression. We will get into more complicated measures later on in this post.
To do this, for each season, I need to organize the data so that each row corresponds to a game. The dependent variable (what we are trying to predict) is the margin of victory from the view of the home team. The independent variables needed will be dummay variables indicating who is home (using a + 1) and who is away (using a -1). Normally you wold also include a dummy variable for neutral site games, however the 2015 season on CFB Reference doesn’t list any info on neutral site games. So even though we have this information for every other season I’m going to have to exclude it since the overall goal of this project is to predict the coming seasons results, so we can’t just ignore we don’t have it for this year.
Let’s get started by reading in the data I’ve pulled from CFB Reference that includes the results of every FBS football game over the last 10 seasons.
library(readr)
library(purrr)
library(dplyr)
library(tidyr)
library(stringr)
library(lubridate)
library(broom)
options(dplyr.width = Inf)
raw_schedule <- read_csv(file = "~/Documents/fb_analysis/Datasets/cfb_schedule_05_15.csv",
col_types = cols(Date = col_date(format = "%b %d, %Y")))
## Need to add the points for the home and away teams and find what season each
## game belongs to
results <- raw_schedule %>%
mutate(Home_Points = ifelse(Winner == Home, Winner_Points, Loser_Points),
Away_Points = ifelse(Winner == Home, Loser_Points, Winner_Points),
Home_MOV = Home_Points - Away_Points,
Season = ifelse(month(Date) == 1, year(Date) - 1, year(Date))) %>%
filter(!is.na(Home_MOV))
| Season | Week | Home | Away | Home_Points | Away_Points | Home_MOV |
|---|---|---|---|---|---|---|
| 2005 | 1 | Arizona State | Temple | 63 | 16 | 47 |
| 2005 | 1 | Cincinnati | Eastern Michigan | 28 | 26 | 2 |
| 2005 | 1 | Connecticut | Buffalo | 38 | 0 | 38 |
| 2005 | 1 | Marshall | William & Mary | 36 | 24 | 12 |
| 2005 | 1 | Tulsa | Minnesota | 10 | 41 | -31 |
| 2005 | 1 | Louisiana-Monroe | Northwestern State | 23 | 27 | -4 |
Now comes the tricky part. I need to turn this long data frame of game results into a wide format that includes the team names as variable names. I’ve written the following helper function to “stack” the teams in each game so that we don’t have to worry about having two team name columns.
organize_game_results <- function(df, ...){
home_teams <- df %>%
select(Season, Game_Num, Home, Home_MOV, ...) %>%
mutate(involved = 1) %>%
rename(Team = Home)
away_teams <- df %>%
select(Season, Game_Num, Away, Home_MOV, ...) %>%
mutate(involved = -1) %>%
rename(Team = Away)
return(bind_rows(home_teams, away_teams))
}
I’m going to do a bit of R Kung Fu but here is my basic approach:
- “Nest” the stacked team
data so that the data is grouped by Season. Since each season’s data is just
stored as a list in a column of the data frame we can use
purrr’smapfunction to perform functions on each season of data seperately. - Use the
spreadfunction from thetidyrpackage to go from a tall to wide format - Use a linear regression to calculate the Massey Rankings
- Use the
tidyfunction from thebroompackage to extract the coefficient values (which are the actual team rankings) - Then unnest each season to get one data frame for our results
season_team_values <- results %>%
organize_game_results %>%
group_by(Season) %>%
nest() %>%
mutate(regression_df = map(data, spread, Team, involved, fill = 0),
model = map(regression_df, ~ lm(Home_MOV ~ . - Game_Num, data = .)),
team_values = map(model, tidy)) %>%
unnest(team_values) %>%
mutate(term = str_replace_all(term, fixed("`"), ""))
| Season | term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|---|
| 2005 | (Intercept) | 3.646571 | 0.5735598 | 6.357787 | 0.0000000 |
| 2005 | Air Force | 31.465096 | 15.7468260 | 1.998187 | 0.0461865 |
| 2005 | Akron | 27.347303 | 15.5560123 | 1.757989 | 0.0793035 |
| 2005 | Alabama | 46.604288 | 15.6858803 | 2.971098 | 0.0030966 |
| 2005 | Alabama-Birmingham | 30.838248 | 15.8030438 | 1.951412 | 0.0515135 |
| 2005 | Appalachian State | 22.981138 | 18.3074848 | 1.255286 | 0.2099059 |
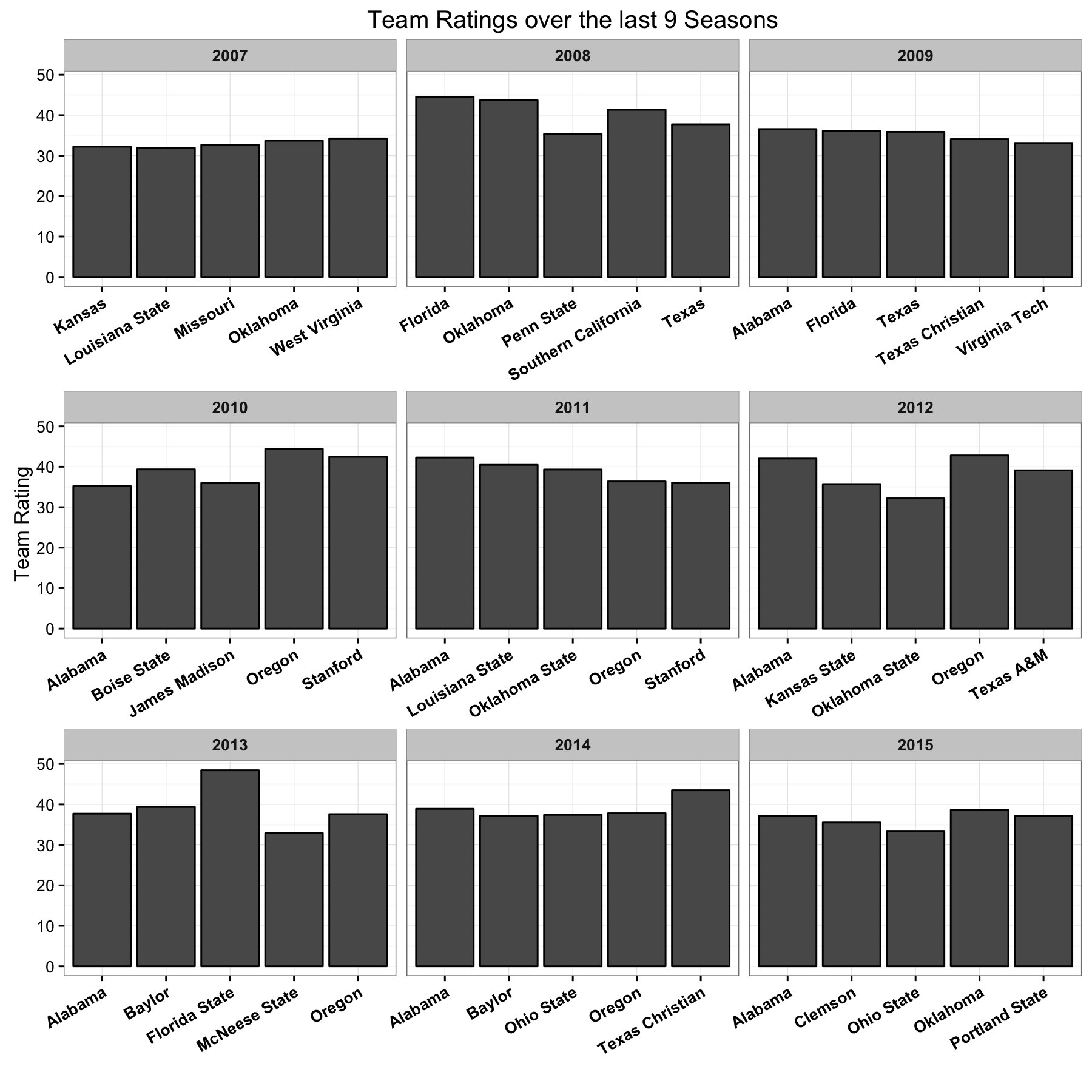
Let’s show the top 5 teams from the last 9 years. To do this I actually have to center the predictions so that the average team rating in each season is
- This is because the regression doesn’t really have any reason to make the average team value zero (or any specific value); it is just concerned with getting difference between team ratings as close to the actial margin of victory, not the rating values themselves.
Problems
If you inspect the results you’ll see that there are some areas where we could improve our results. Here is a list off the top of my head:
- We don’t adjust for blowouts at all
- We don’t adjust for teams who only play 1 or 2 games all season. For example, Portland State beat two very bad teams in 2015 but those were their only games so they are rated as one of the best teams in the country. We could just consider all teams who only showed up 1-2 times as one team, sort of as a placeholder for “FCS” teams (the lower division of CFB).
- We don’t use a penalized regression to regularize our results at all
- We don’t include any team priors from the previous season.
While I certainly believe all of these areas could help improve our results I’d like a way to know for sure. Since the goal of this post is to determine how good each team was in a season we can just test that. If our team ratings accurately predict the results of games between teams then we can assume that the ratings reflect the true quality of teams.
What we don’t want to do is use the same underlying games to both generate and test the accuracy of the team rankings, then we would be rewarding methods that overfit to the season results and not the true underlying team quality. So we will have to generate our team rankings and then test their accuracy on different sets of games. I’m going to do this using cross validation which is a popular way to test the accuracy of models while avoiding overfitting.
Let’s find the accuracy of this base method we have already used. I’m using
a helper function called safe_pred which you can find in the raw R file I
used to write this post. It basically helps make predictions when a team
only shows up in the training or test data but not both, which normally
would cause an error. If there is a game in the test set that we can’t
predict then I just remove it which biases our results some. Since this is,
well was, supposed to be a quick post I’m cool with that for now.
K <- 4 # number of cross validated folds
cv_results <- results %>%
mutate(fold_id = sample(1:K, size = n(), replace = T)) %>%
organize_game_results(fold_id) %>%
group_by(Season) %>%
nest() %>%
crossing(fold = 1:K) %>%
mutate(train = map2(data, fold, function(df, fold_num) filter(df, fold_id != fold_num)),
test = map2(data, fold, function(df, fold_num) filter(df, fold_id == fold_num)),
regression_df = map(train, spread, Team, involved, fill = 0),
test_df = map(test, spread, Team, involved, fill = 0),
model = map(regression_df, ~ lm(Home_MOV ~ . - Game_Num - fold_id, data = .)),
preds = map2(model, test_df, safe_pred),
error = map_dbl(preds, function(df) mean((df$Home_MOV - df$pred)^2))) %>%
group_by(Season) %>%
summarize(mean_mse = mean(error), sd_mse = sd(error))
c(mean(cv_results$mean_mse), mean(cv_results$sd_mse))
## [1] 262.15520 21.53612
So that’s our baseline Mean Squared Error.
Let’s try and beat it using the 2nd idea I had. The first is kind of arbitrary (what do we define as a blowout?) and the fourth we will focus on in the actual prediction model we are trying to build, so I don’t think it’s needed yet.
game_list <- results %>%
mutate(fold_id = sample(1:K, size = n(), replace = T)) %>%
organize_game_results(fold_id)
bad_teams <- game_list %>%
count(Season, Team) %>%
mutate(bad_team = n <= 2)
fcs_fix_results <- game_list %>%
left_join(bad_teams, by = c("Season", "Team")) %>%
mutate(Team = ifelse(bad_team, "FCS", Team)) %>%
select(-n, -bad_team) %>%
group_by(Season) %>%
nest() %>%
crossing(fold = 1:K) %>%
mutate(train = map2(data, fold, function(df, fold_num) filter(df, fold_id != fold_num)),
test = map2(data, fold, function(df, fold_num) filter(df, fold_id == fold_num)),
regression_df = map(train, spread, Team, involved, fill = 0),
test_df = map(test, spread, Team, involved, fill = 0),
model = map(regression_df, ~ lm(Home_MOV ~ . - Game_Num - fold_id, data = .)),
preds = map2(model, test_df, safe_pred),
error = map_dbl(preds, function(df) mean((df$Home_MOV - df$pred)^2))) %>%
group_by(Season) %>%
summarize(mean_mse = mean(error), sd_mse = sd(error))
c(mean(fcs_fix_results$mean_mse), mean(fcs_fix_results$sd_mse))
## [1] 264.92329 24.70148
Well that wasn’t even an improvement, I guess since by definition those teams don’t appear too often it really wouldn’t make that much of a difference. What about using a penalized regression like ridge regression to reduce the size of the coefficients? Once again we are going to need a helper function to help us accomplish this. Also there is a bit of weird stuff we should focus on more if we had time. For example we use cross validation to split the data and then more cross validation on that to find the optimal lambda value to use in the ridge regression to predict on the holdout data for that fold. I don’t love this idea but it’s also quick and easy so, we will worry about it later.
ridge_results <- game_list %>%
group_by(Season) %>%
nest() %>%
crossing(fold = 1:K) %>%
mutate(train = map2(data, fold, function(df, fold_num) filter(df, fold_id != fold_num)),
test = map2(data, fold, function(df, fold_num) filter(df, fold_id == fold_num)),
regression_df = map(train, spread, Team, involved, fill = 0),
test_df = map(test, spread, Team, involved, fill = 0),
model = map(regression_df, ridge_fit),
preds = map2(model, test_df, ridge_pred),
error = map_dbl(preds, function(df) mean((df$Home_MOV - df$pred)^2))) %>%
group_by(Season) %>%
summarize(mean_mse = mean(error), sd_mse = sd(error))
c(mean(ridge_results$mean_mse), mean(ridge_results$sd_mse))
## [1] 686.80903 84.38344
Wow, that’s way worse than the linear regression results.
Conclussions
So there you have it, we’ve shown a way to generate ratings for team quality
in a season and shown that those are about as good as we could do using the
limited data we do have. I’d love to do some more analysis around how
variable the estimates are and other predictive models but that’s not really
the goal of this poist. Also I’m pretty proud of getting that grouped cross
validation code to work using nested data frames and the purrr package so
I’ll call it a day. As always please reach out if you have any comments or
questions!